15 Clustering

Clustering
Unsupervised Learning
K-means
This lecture discusses the basics of clustering, focusing on the k-means algorithm. It covers the algorithm’s initialization, convergence, and the concept of local minima.
Author

Jiuru Lyu

Published

April 20, 2025

Partitional Clustering

  • Basic idea: group similar points.
  • Goal: Given a set of examples \(D=\qty{\va x^{(i)}}_{i=0}^N\), \(\va x^{(i)}\in\R^d\).
    • Assign similar points to the same clusters, and
    • Assign dissimilar points to different clusters.
  • Measure dissmilarity: Euclidean distance: \[\norm{\va x^{(i)}-\va x^{(j)}}^2.\]
  • Notation:
    • \(C\): cluster, a set of point indices
    • \(\va z^{(j)}\): representative example, cluster centroid.
      • Partition \(\R^d\) into \(k\) convex cells.
      • \(z_j=\dfrac{1}{\abs{C_j}}\sum_{i\in C_j}\va x^{(i)}\).
      • \(C_j=\qty{i=1,\dots,N,\quad\text{where the closest representative example to }\va x^{(i)}\text{ is }\va z^{(j)}}\)
    • Given \(C_j\), we can find \(z_j\), and vice versa.
Figure 1: Cluster
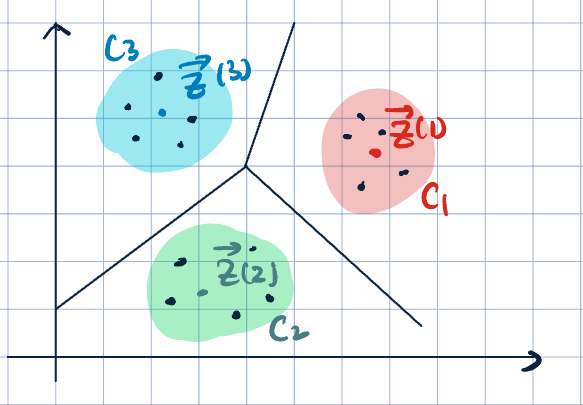
  • Objective: Intertia/Within-Cluster Sum of Square/Intra-Cluster Distance \[ \min_{\textcolor{blue}{\substack{C_1,\dots,C_k\\\va z^{(1)},\dots,\va z^{(k)}}}}\textcolor{red}{\sum_{j=1}^k}\textcolor{teal}{\sum_{i\in C_j}}\norm{\va x^{(i)}-\va z^{(j)}}^2 \]
    • \(\dsst\min_{\textcolor{blue}{\substack{C_1,\dots,C_k\\\va z^{(1)},\dots,\va z^{(k)}}}}\): Find clusters and their centroids.
    • \(\dsst\textcolor{red}{\sum_{j=1}^k}\): Sum over all clusters.
    • \(\dsst\textcolor{teal}{\sum_{i\in C_j}}\): Sum over points in each cluster.
    • This problem is NP-hard.
    • We have efficient heuristics to find local optimum.
\begin{algorithm} \caption{K-Means Clustering (Alternating Minimization)} \begin{algorithmic} \State{Initialize $\va z^{(1)},\dots,\va z^{(k)}$ randomly.} \While{not converged} \For{$j=1,\dots,k$} \State{$C_j=\qty{i=1,\dots,N,\text{ where the closest representative example for }\va x^{(i)}\text{ is }\va z^{(j)}}$} \EndFor \For{$j=1,\dots,k$} \State{$\dsst\va z^{(j)}=\dfrac{1}{\abs{C_j}}\sum_{i\in C_j}\va x^{(i)}$} \EndFor \EndWhile \end{algorithmic} \end{algorithm}

Example 1 (K-Means Example)  

Figure 2: K Means
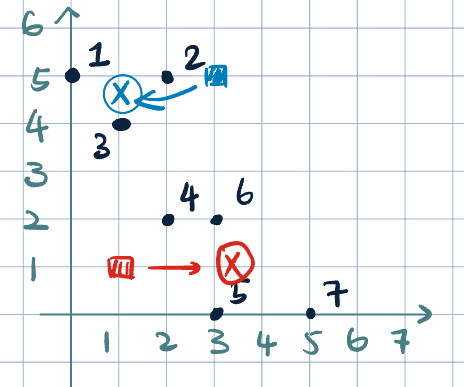
  • \(k=2\)
  • Initialization: \(\textcolor{blue}{\va z^{(1)}=(3,5)}\) and \(\textcolor{red}{\va z^{(2)}=(1,1)}\)
  • Fix \(\va z^{(j)}\). Make assignment:
Point \(L^2\) Distance to \(\textcolor{blue}{\va z^{(1)}}\) to \(\textcolor{red}{\va z^{(2)}}\) Assignment
1 \((0,5)\) \(3\) \(\sqrt{17}\) \(\textcolor{blue}{C_1}\)
2 \((2,5)\) \(1\) \(\sqrt{17}\) \(\textcolor{blue}{C_1}\)
3 \((1,4)\) \(\sqrt{5}\) \(3\) \(\textcolor{blue}{C_1}\)
4 \((2,2)\) \(\sqrt{10}\) \(\sqrt{2}\) \(\textcolor{red}{C_2}\)
5 \((3,0)\) \(5\) \(\sqrt{5}\) \(\textcolor{red}{C_2}\)
6 \((3,2)\) \(3\) \(\sqrt{5}\) \(\textcolor{red}{C_2}\)
7 \((5,0)\) \(\sqrt{29}\) \(\sqrt{17}\) \(\textcolor{red}{C_2}\)
  • Update centroid:
    • \(\textcolor{blue}{\va z^{(1)}=(1, 4.67)}\)
    • \(\textcolor{red}{\va z^{(2)}=(3.25, 1)}\)
  • We are converged already because redo the iteration will not change the assignment and clusters anymore.
  • Convergence:
    • Clusters/centroids stop changing.
      If ties are not broken consistently, we may cycle. If it cycles, we know we converged.
    • \(k\)-means is guaranteed to converge (to local optimum), but we may not necessarily converge to the global optimum.
  • Initialization:
    • Randomly
    • \(k\)-means\(++\): accounts for distribution of \(\va x\) in \(\R^d\). This approach tries to “spread it out” more.
    • In general, we repeat \(k\)-means multiple times. We choose clustering solution with lowest inertia.
  • Choosing \(k\):
    • In some applications, \(k\) will be given.
    • Use validation data.
    • The “elbow” method: plot inertia vs. \(k\). Choose \(k\) where the curve starts to flatten out.
Figure 3: Elbow Method

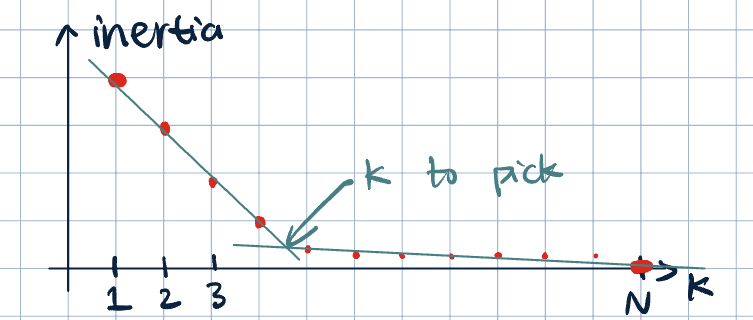
Remark 1 (The Elbow Plot). If \(k=N\), every point forms its own cluster. \[\sum_{j=1}^N\sum_{i\in C_j}\norm{\va x^{(i)}-\va z^{(j)}}^2=0\implies \va z^{(j)}=\va x^{(i)}.\]

Back to top