5 Logistic Regression

This lecture introduces the logistic regression model, which is used for binary classification. We will discuss the sigmoid function, the likelihood function, and the cost function.

Motivation

• The problem: Given binar labels \(y\in\qty{-1,+1}\). We want to predict the probability of positive class, \(\hat y\in[0, 1]\).
• How to make a linear model output a probability? We already have \(\va\theta\cdot\va x\in(-\infty,\infty)\).
  • Apply a sequashing function: \(\sigma(\va\theta\cdot\va x)\in[0,1]:\R\to[0,1]\).
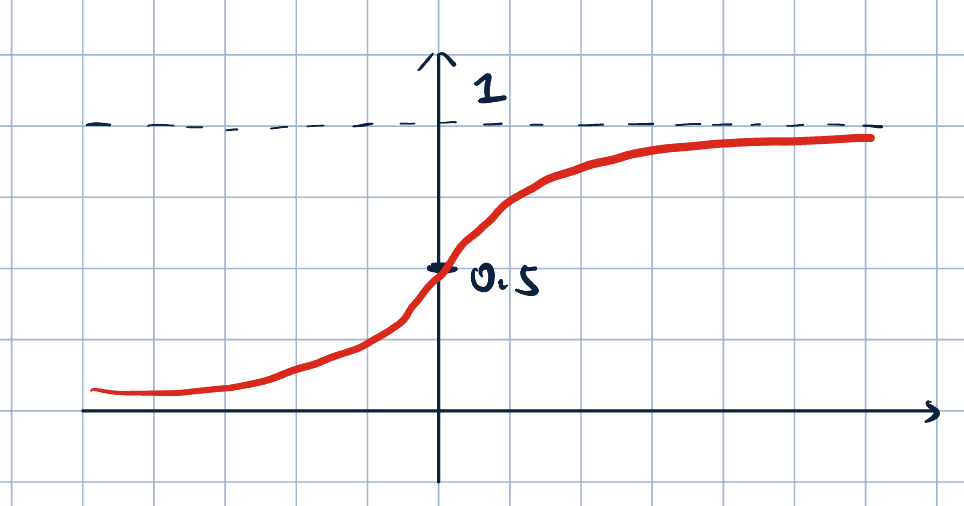
  • We will use a sigmoid function*: \[\sigma(z)=\dfrac{1}{1+e^{-z}}\]
    • Range of sigmoid:
      • for \(z\to\infty\), \(\sigma(z)\to 1\)
      • for \(z\to-\infty\), \(\sigma(z)\to 0\)
      • \(\sigma(0)=0.5\)
    • Useful properties:
      • \(\sigma(-z)=1-\sigma(z)\)
      • \(\sigma'(z)=\sigma(z)(1-\sigma(z))\)
      • continuous
      • differentiable
      • not convex

Figure 1: Sigmoid Function

Logistic Regression

• Logistic Regression: \[ h(\va x;\va\theta)=\sigma(\va\theta\cdot\va x)=\dfrac{1}{1+e^{-\va\theta\cdot\va x}} \]

• How to train this classifier? What loss function should we use?

  • What we want: \(\sigma(\va\theta\cdot\va x)\) should be the probability of positive class: \(\P[y=+1\mid\va x]\).
  • Idea: If \(\sigma(\va\theta\cdot\va x)\) is truely the probability, then we can use it to wrtie down the likelihood of the training data \(\qty{\va x^{(i)}, y^{(i)}}_{i=1}^N\).
    • For each example \(\va x^{(i)}\), the likelihood of seeing its label to be \(y^{(i)}\) is \[ \P[y=y^{(i)}\mid \va x^{(i)};\va\theta]=\begin{cases}\sigma(\va\theta\cdot\va x^{(i)})&\quad\text{if }y^{(i)}=+1\\\underbrace{1-\sigma(\va\theta\cdot\va x^{(i)})}_{=\sigma(-\va\theta\cdot\va x^{(i)})}&\quad\text{if }y^{(i)}=-1\end{cases}=\sigma(y^{(i)}\va\theta\cdot\va x^{(i)}) \]
    • Since each training example is generated independently, \[\P\qty[\qty{y^{(i)}}_{i=1}^N\mid\qty{\va x^{(i)}}_{i=1}^N;\va\theta]=\prod_{i=1}^N\sigma(y^{(i)}\va\theta\cdot\va x^{(i)})=\prod_{i=1}^N\dfrac{1}{1+e^{-y^(i)\va\theta\cdot\va x}}\]
  • Goal: Find \(\va\theta^*\) such that maximizes the likelihood of the training data: \[\va\theta^*=\argmax_{\va\theta}\prod_{i=1}^N\dfrac{1}{1+e^{-y^{(i)}\va\theta\cdot\va x^{(i)}}}\]
    • Take the log: \(\prod\to\sum\): \[\argmax_{\va\theta}\log\prod_{i=1}^N\dfrac{1}{1+e^{-y^{(i)}\va\theta\cdot\va x^{(i)}}}=\argmax_{\va\theta}\sum_{i=1}^N\log\qty(\dfrac{1}{1+e^{-y^{(i)\va\theta\cdot\va x^{(i)}}}})\]
    • Take the negative: \[\argmax_{\va\theta}\sum_{i=1}^N\mathrm{loss}=\argmin{\va\theta}\qty(\sum_{i=1}^N-\log\qty(\dfrac{1}{1+e^{-y^{(i)}\va\theta\cdot\va x^{(i)}}}))=\argmin_{\va\theta}\sum_{i=1}^N\log\qty(1+e^{-y^{(i)}\va\theta\cdot\va x^{(i)}})\]

Definition 1 (Logistic Loss:) \[\mathrm{loss}_\text{log}\qty(\va x^{(i)}, y^{(i)};\va\theta)=\log\qty(1+e^{-y^{(i)}\va\theta\cdot\va x})\]

Figure 2: Logistic Loss

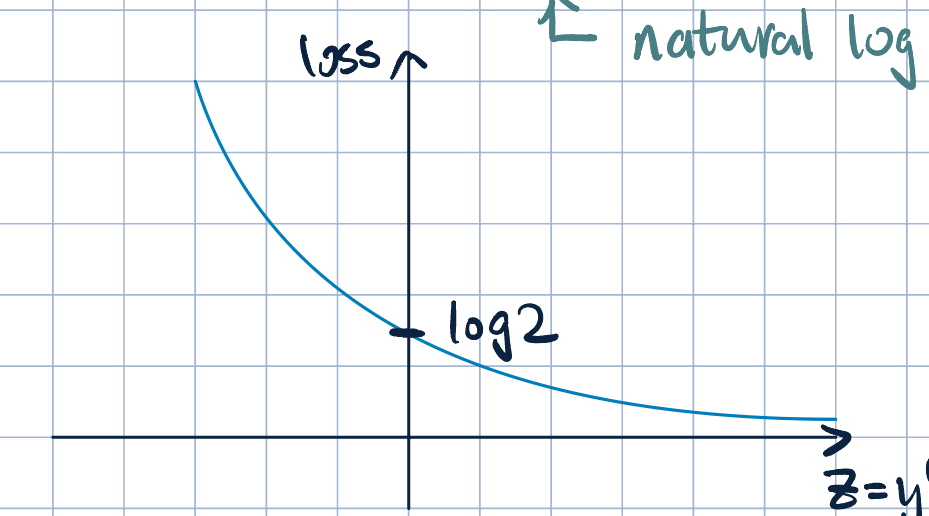
This loss is: - continuous - Differentiable, and - Convex

So, we can use SGD to minimize it.

SGD Update Rule

\[ \begin{aligned} \grad_{\va\theta}\log\qty(1+e^{-y^{(i)}\va\theta\cdot\va x^{(i)}})&=\dfrac{1}{1+e^{-y^{(i)}\va\theta\cdot\va x^{(i)}}}\qty(e^{-y^{(i)}\va\theta\cdot\va x^{(i)}})\grad_{\va\theta}\qty(-y^{(i)}\va\theta\cdot\va x^{(i)})\\ &=\dfrac{1}{e^{y^{(i)}\va\theta\cdot\va x^{(i)}}+1}\qty(-y^{(i)}\va x^{(i)})\\ &=\sigma\qty(-y^{(i)}\va\theta\cdot\va x^{(i)})\qty(-y^{(i)}\va x^{(i)})\\ &=-y^{(i)}\va x^{(i)}\qty(1-\sigma(y^{(i)}\va\theta\cdot\va x^{(i)})). \end{aligned} \]

So, the update rule is: \[ \begin{aligned} \va\theta^{(k+1)}&=\va\theta^{(k)}-\eta_k\eval{\qty[-y^{(i)}\va x^{(i)}\qty(1-\sigma(y^{(i)}\va\theta\cdot\va x^{(i)}))]}_{\va\theta=\va\theta^{(k)}}\\ &=\va\theta^{(k)}+\eta_ky^{(i)}\va x^{(i)}\qty(1-\sigma(y^{(i)}\va\theta^{(k)}\cdot\va x^{(i)})) \end{aligned} \]

• There’s no closed-form solution for logistic regression in general case. However, since the empirical risk function is convex, \(\exists\) unique global minimum. When there are linearly dependent (redundant) feature, there are infinitely many equally good local minima.

• If the data is linear separable, \(\|\va\theta\|=\infty\) is bad. So, we need to add regularization.