8 Shortest Path

Coding
Java
Algorithm
Shortest Path
This lecture introduces the concept of shortest path in graphs, including BFS for unweighted graphs and Dijkstra’s algorithm for weighted graphs.
Author

Jiuru Lyu

Published

May 16, 2024

Beyond Connected Graphs

  • If the graph is not connected, we can still complete the graph traversal by calling DFS() method.
Algorithm
    Randomly select a vertex from the unvisited vertices
    Apply DFS
    Repeat the process untill all vertices are visited

BFS to Find Shortest Path in Unweighted Graph

Definition 1  

  • In unweighted graphs, the length of a path is defined as the number of edges in this path.
  • Length of the shortest path between two vertices is known as their distance.
  • BFS can find the shortest paths.
    • BFS is a process of “iteratively visiting the unvisited neighbors closest to source.”
    • BFS tree records the shortest path from the starting vertex to all other vertices.
    • Example: the BFS tree is marked in the blue and solid arrows in the following graph.
Figure 1: BFS Tree

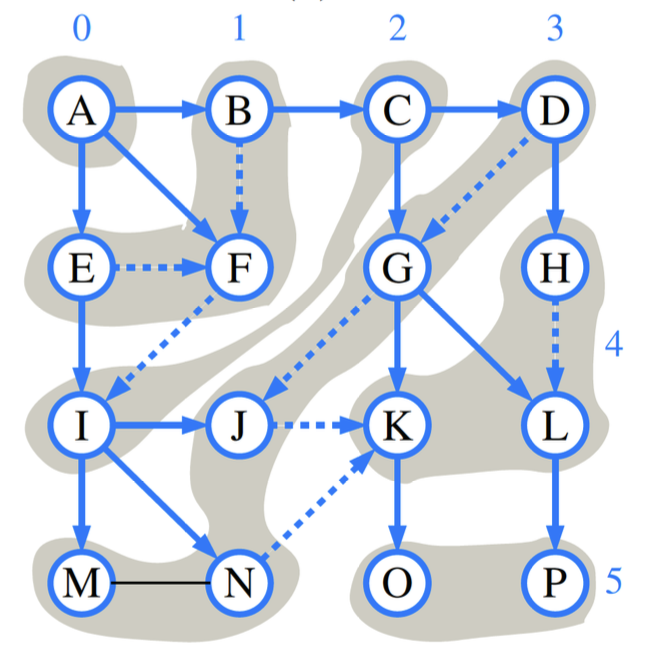
Shortest Path Search in Weighted Graph

Definition 2  

  • We will consider non-negative weight in this lecture.
  • The weight of an edge \(e=(u,v)\) is denoted as \(w(u,v)\) or \(w(e)\).
  • In weighted graph, the length of a path \(P\) is the sum of the weights of the edges in \(P=((v_0,v_1), (v_1,v_2),\dots,(v_{k-1},v_k))\): \[w(P)=\sum_{i=0}^{k-1}w(v_i,v_{i+1}).\]
  • Distance between two vertices denotes the length of the shortest path between them.
  • In a weigthed graph, the general idea of finding the shortest path is to:
    • Start from a source vertex, initialize all the vertices’ distances to starting vertex as infinity
    • Visit the univisted closest vertex
    • Update the distance of the neighbors
    • Repeat the process until all vertices are visited
  • Claim: Through the process above, once a vertex is visited, its currently recorded distance is already the shortest distance to the starting vertex.
Proof (by contradiction).

Assume the above claim is false: “Suppose the currently visited vertex \(z\) is the first one whose recorded distance is not the shortest path length.”

Then, one of the following situation must happens:

  • Situation 1: All vertices in the path are visited vertices.
  • Situation 2:Shortest path goes through some unvisited vertices.

If situation 1 happens, assume vertex \(v\) is the predecessor of \(z\) in the shortest path, then we should have already examined this path while visiting \(v\) and its neighbors and recordes this as the distance. This leads to contradiction.

If situation 2 happens, then let’s assume vertex \(y\) is the first unvisted vertex in the shortest path and vertex \(x\) is \(y\)’s predecessor in the shortest path. So, vertex \(x\) is already visited before visiting \(z\) and \(x\)’s neighbor \(y\) has smaller distance to \(s\) (the source vertex) than \(z\), so \(y\) should be visited earlier than \(z\). This also leads to contradiction.

Because of the contradictions, the statement cannot be false. The proof is therefore completed. \(\qquad\blacksquare\)

  • Dijkstra’s Algorithm
Algorithm MST(s):
  INPUT: start vertex s;
  OUTPUT: all vertices' distances to s;

  START:
  Initialize all the vertices' distances to the starting vertex as infinity
  while there is still unvisited vertex do {
    1. visit the unvisited closest vertex;
    2. update this vertex’s neighbors’ distances;
  }
Back to top