10 Minimum Spanning Tree (MST)

This lecture introduces the minimum spanning tree algorithm

Introduction

• Claim: Every connected graph has at least one spanning tree.

Definition 1 Minimum Spanning Tree: the spanning tree with the smallest sum of edge weights.

• Application of MST:

  • Minimal total cost of edges to ensure the connectivity of the network.
  • For example, telecommunication networks, computer networks, transportation networks, etc.

• Key Property of MST:

  • Fact: In a connected graph, partition the set of vertices into any two groups, there must be \(\geq1\) edges connecting these groups.
  • Property: Among these edges (connecting these groups), the MST of this graph must include the edge with the smallest weight.

  Proof (by contradiction).

  

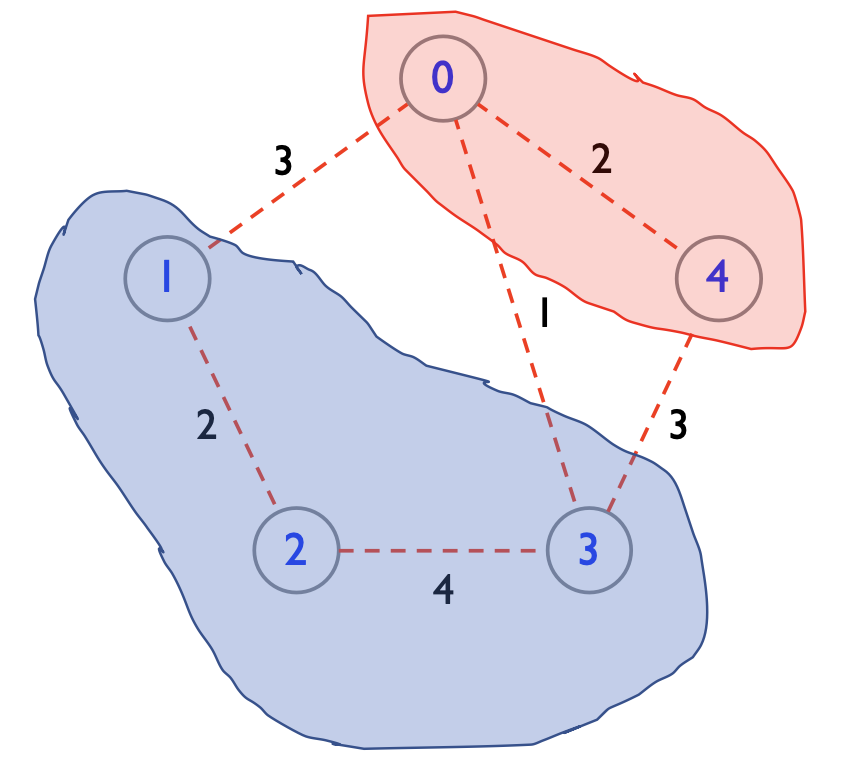
  Suppose among \((0,1)\), \((0,3)\), \((3,4)\), the edge \((0,3)\) has the smallest weight but is not included in the MST. Then, one of \((0,1)\) and \((3,4)\) must be in the MST to ensure the two parts are connected.

  However, if we add \((0,3)\) into the MST, we will therefore get a graph with a cycle involving either \((0,1)\) or \((3,4)\). Deleting such an edge, we form again a spanning tree. This spanning tree has a smaller weight than our previously defined MST. Therefore, our assumption is wrong. The smallest weight must be involved in the MST. \(\qquad\blacksquare\)

  • Generalization: So, among the edges spanning two groups, the one with the smallest weight must be in the MST:
    • Smallest weight
    • Spanning two groups

Prim’s Algorithm (Prim-Jarnik Algorithm)

• Idea:
  • Find edges spanning two groups.
  • Find the edges with the smallest weight (aka, visit the unvisited vertex closed to the current group).
  • Update the groups
  • Repeat the process until all vertices are visited.

Algorithm (Prim's Algorithm):
    INPUT: an undirected, weighted, connected graph
    OUTPUT: a tree
    INITIALIZATION: 
        1. Randomly pick up a starting vertex
        2. Initialize all vertices' distances to the starting vertex
    
    while (thre is still unvisted vertex) {
        1. visit the unvisted vertex closest to the tree
        2. update this vertex's unvisited neighbors' distances to the tree. 
    }

• This algorithm is very similar to Dijkstra’s algorithm. The only difference is that Prim’s algorithm will update the tree’s distance to the unvisited vertex, while Dijkstra’s algorithm will update the distance to the starting vertex.

Kruskal’s Algorithm

• Idea:
  • First, find the edge with the smallest weight.
  • Then, find if this edge indeed connects two groups.
  • If so, add this edge to the MST.
  • Repeat the process until all vertices are visited.

Algorithm (Kruskal's Algorithm):
    INPUT: an undirected, weighted, connected graph
    OUTPUT: All the selected edges that form an MST
    INTIALIZATION:
        1. initialize an empty edge list;
        2. initialize each vertex as a component;
    
    while (edge list has less than n-1 edges) {
        1. get the smallest-weighted unvisted edge;
        if (this edge spans two different components) {
            2.1 add this edge to the edge list;
            2.2 union these two components;
        }
    }

Comparison of Two Algorithms

	Kruskal Algorithm	Prim’s Algorithm
Step 1	find the edge with the smallest weight	find the edges spanning two groups
Step 2	tell if it spans two groups	find the edges with the smallest weight
Step 3	update the groups	update the groups
Time Complexity ($N = $ number of vertices and $M = $ number of edges)		\(\mathcal{O}((M+N)\log{N{}})\)